赤道の位置と緯度・経度
さて今回から授業を進めていきます。前回授業で伝えた必要となる教材はありますか?そして今回は、前回描いてもらった世界地図も使っていきます。ありますか?いろいろな世界地図が出来ていましたね…場合によってはアフリカ大陸が消失している場合もあるかと思います。アフリカ大陸がなくなったら大陸は4つですね、その場合オリンピックは4輪になってしまいますね…5輪はそもそも大陸5つの平和の祭典なので、大陸の数と対応しています。さて、前回の授業で私自身も世界地図を描きましたが、世界地図を描くときのコツがあります。それは赤道の位置を揃える事です。30秒ほど時間を取りますので自分の描いた地図に赤道を描き込んでみて下さい。どうですか?
さて引けましたか?場合によっては日本に赤道が通っている地図も産まれているかもしれませんが…この位置が正しいとそれなりに見えてきます。正しい地図としては、以下の3か所に赤道が通るようにしてみて下さい。一つ目がアフリカ大陸の凹みのすぐ下、二つ目が東南アジアのマレー半島の先のシンガポールあたり、三つ目が南アメリカ大陸の東の出っ張りのすぐ上あたりです。赤道の位置は実はとても大切な情報です、今後問題を解くときに世界地図を見たらまず赤道を描き込む癖をつけてください。さて赤道が通る場所、南アメリカ大陸では「エクアドル」という国の真上を通ります。この国名は英語で赤道を意味する「equator」が語源ですので、当然赤道直下にあります。ところがアフリカ大陸を見ると、「赤道ギニア」という国がありますが赤道直下ではないですね。嘘ですね。これはどうも「赤道に近い方のギニア」という意味があるようです。アフリカにはギニアという国がいくつかあります。ギニア、赤道ギニア、ギニアビサウ…ギニアという単語は諸説あるようですが「黒」という意味があるそうです。つまり「黒人の地」という意味ですね。だからみんな「ギニア」なんですね。ちなみに「赤道」というのは古代中国の天体観から来た言葉です。同様に星の動きなどは黄色を使った「黄道12星座」と表したりしますね。
さて、赤道はちょうど地球の一番膨らんでいるところを結ぶ線と言えますが、地球は便宜上、南北方向を表す緯度と、東西方向を表す経度で位置を定めます。赤道は横線なので南北方向を示す緯線と呼べますね。赤道は緯度でいうと何度でしょうか?そして緯線は北極・南極まで続きますが、極は緯度何度ですか?30秒取るので確認してみて下さい。
大丈夫でしょうか。赤道は緯度0度、極は90度ですね。北半球が北緯、南半球が南緯で表されます。スタート地点となる赤道は地球上で一番膨らんでいるところ、これはわかりやすいですが、経度はどうでしょうか?スタート地点は正直どこでも良いですね、経度0度はどこと定められていますか?そうです、イギリスにある旧グリニッジ天文台を通る線と定められています。これはフランスと揉めたらしいんですが、結局はイギリスがその名誉を勝ち取ったそうですね。ちなみに旧グリニッジ天文台に行ったことがありますが、あまりおすすめしません。天文台なので丘の上にあるのに交通手段がなくて走って登りましたが、想像以上にしょぼかったです。観光客もほとんどいませんでしたね、知名度があるのは日本だけなんじゃないかな。さて、0度はグリニッジ天文台を通る線、この線は特別に名称がついています。本初子午線です。子午線ってなんでしょうね?これは十二支と関係しています。十二支を円形に配置すると、一番上が子、一番下が午となります。つまり子午線とは南北方向の線という事です。ちなみにかつて日本はこの十二支を時刻としても利用していました。子の刻が午前0時を表し、24時間を十二支で表すと、午の時間は何時でしょうか?ちょうど正午となります。さらにそれより前を午前、午後と表す訳ですね。さらに別の話で、子の刻の次は丑の刻が来ます。時刻としては午前1時から3時まで、一番人気の無い時間です。こんな時間にお寺の林に行くと、藁人形を持って白装束を来た人が釘で人形を打ち付けている訳です。これが丑の刻参り、草木も眠る丑三つ時というやつですね。
話は脱線しましたが本初子午線の話から、ここが経度0度の線となります。これより東が東経、西が西経です。すると一周周った180度の場所は一致します。東経・西経180度の線はなんと呼ばれるでしょうか?これが日付変更線と呼ばれるものです。この線を境に日付が違い、日付変更線より西側が一日が始まるのが早く、東側が遅くなります。本初子午線は大きな影響はないですが、日付変更線が国をまたいでいると大混乱となってしまうので国を避ける形で引いてありますね。こう見ると日本は、世界的に見てもかなり早く一日が始まる国だという事がわかるかと思います。こうなると面白い現象が発生したりします。これは友人に実際起こったことなのですが、その友人は年越しをニューヨークで過ごしたいと思って航空機チケットを取った。ニューヨークの年越しはタイムズスクエアに巨大なボールが出現して、年越しの瞬間になるまで少しずつ地面に近づいていく仕様になっています。ボールが地面についた瞬間、周りのビルから一斉に花火が上がるんですね。それが見たいと。でも仕事が忙しくて、取れた航空チケットが12月31日の東京21時発のチケットだった。そこからニューヨークに向かうとどうなるか。実は日付変更線をまたぐ少し前に1月1日を迎えてしまうんだそうです。機内でハッピーニューイヤーを聞きながら飛ぶそうなんですが、日付変更線を超えた瞬間に12月31日に戻るんだそうです。面白いですね。
さてまた脱線してしまいましたが、緯度は90度まで、経度は180度まであります。緯度に関しては、赤道に近い地域は低緯度地域、極に近い地域は高緯度地域と呼びます。また経度に関しては、日本の兵庫県明石市を通る東経135度の標準時子午線も併せて思い出しておいてください。
地図の種類
さて、ここまでは今後地理をやっていく上で必要となる基礎的な知識の復習です。これらを踏まえて地図というものをもう一度考えてみましょう。では前回描いてもらった世界地図をもう一度見てみて下さい。なぜ「世界地図を描いてね」と言った時、皆一様に四角の地図を描くのでしょうか?1分時間を取るのでもう一度考えてみて下さい。
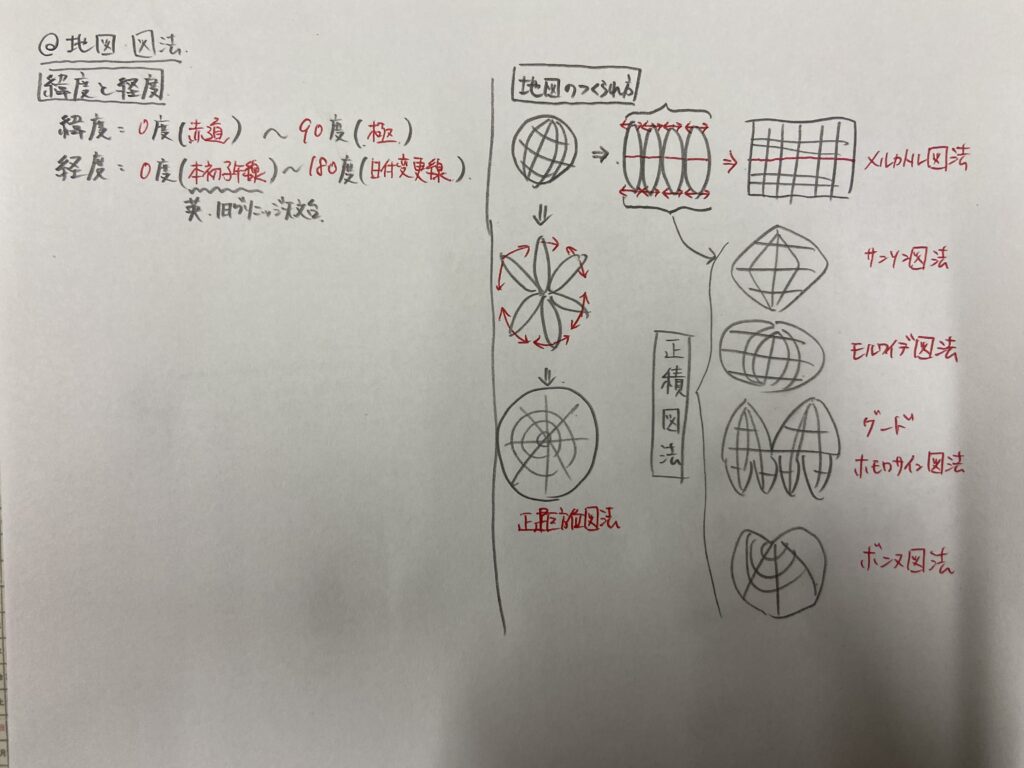
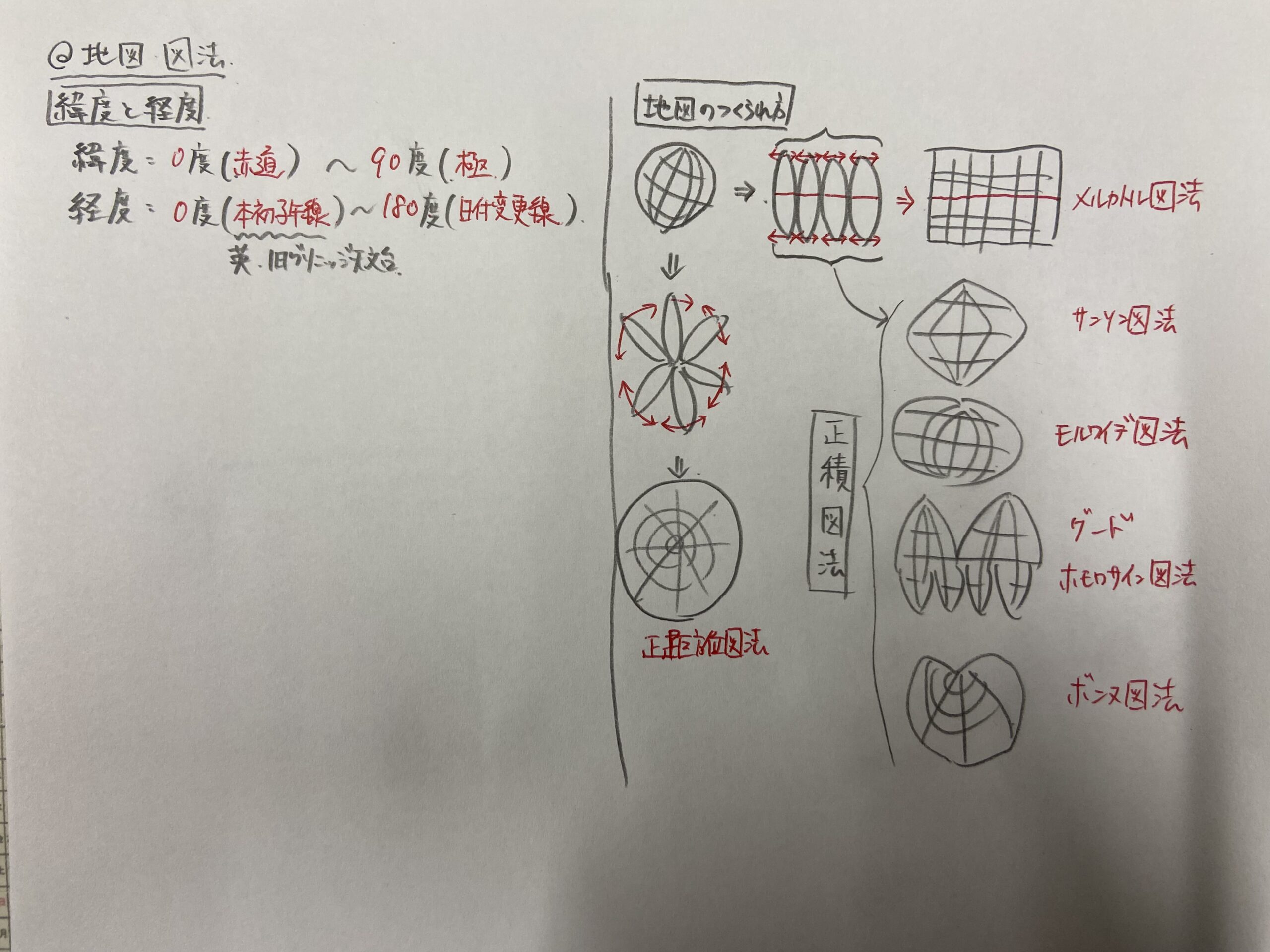
考えられましたでしょうか?じゃあ何人かに聞いてみようと思います。…様々出てきましたが、中々これだという答えにはならないですね。それではヒントとして、そもそも四角の地図はどうやって出来ているのかを教えておこうと思います。地図には様々な種類があります。四角から丸、ピーナッツのような形からハート形まで、それぞれの地図は全て何かが実際の地球とは違っています。球体を平面にしているのだから当然ですね。地球を縦に、皮をむいたように赤道がつながるように並べると仮定しましょう。そうすると楕円形のものが並びます。この時、北極と南極の付近はどうしても空白が出来てしまいます。これを引き延ばして四角にするとよく見る地図、いわゆるメルカトル図法と呼ばれる地図となります。ただしこの地図は、極付近、高緯度地域を無理やり伸ばしているので、高緯度地域は実際よりかなり大きく描かれることになります。つまり面積は正しく表せていません。高緯度地域がどれくらい広げられているのか?以下の画像がよくこれを表しています。
またこのサイズの違いを体感できるサイトがあります。タブレットで「true size of」と入力してみて下さい。このサイトでは、メルカトル図法であらわされた国が実際どれくらいのサイズなのか比較できるサイトになっています。例えば「Japan」と入れれば日本を移動できます。色々移動させてみて下さい、意外に日本は大きいことがわかりますよ。また、「Greenland」と入れてもらえれば、実際はかなり小さいことがわかります。メルカトル図法ではアフリカ大陸とほとんど同じくらいの大きさですが、実際にはずいぶん小さいことがわかりますね。
さてメルカトル図法で面積は正しく表せない事がわかりました。面積を正しくあらわすためには、引き延ばすのではなく絞る必要があります。極付近を一点に集約して地図を作ると、コマのような形になります。これがサンソン図法の地図です。この地図は面積の比率が正しく表されていますが、今度は高緯度地域が見づらくなってしまいました。面積の比率を正しく表し、かつ高緯度地域も見やすくするために縦方向の間隔を調整して作られたのが楕円形のモルワイデ図法の地図です。これなら高緯度も少しは見やすくなりましたね。これらは面積の比率が正しく描かれているので正積図と呼ばれます。正積図の中には、人が住んでいない部分は大胆にカットして、サンソン図法とモルワイデ図法を組み合わせて作った地図もあります。これがピーナッツのような形をしたグード、またはホモロサイン図法の地図です。また、たびたび問題となる高緯度地域を中心に面積が正しく、かつしっかり描かれた地図というものも考え出されました。これがハート型の地図、ボンヌ図法による地図です。これは例えばロシアのような高緯度地域の国の天気予報などでも使用されているようです。もしメルカトル図法で描かれた地図で天気予報地図を作ると、極近くの雲だけやたら早く動いてしまいますからね。
また、剥いた地球の並べ方を変えると違った地図を作ることもできます。先ほどは赤道が接するように並べましたが、今度はミカンの皮のように並べてみます。そうするとヘタの部分はくっついていて、花びらのような並び方になります。ヘタから遠い所は空白だらけですが、これを無理やり伸ばすと丸い地図が出来ます。この地図はヘタからの距離が同心円状に広がりますね。なので中心の点からの距離を正しく表す、かつ地球の丸みを考慮したときの方角も正しく表す事が出来ます。これを正距方位図法と呼びます。距離は正しく表せますが、こちらも無理やり引っ張っているので面積は正しくありません。
こう見るとやはり、どの地図を使っても何かがおかしく何かが合っているという事がわかります。とするならば、やはりなぜ四角の地図がいわゆる「世界地図」なのかが疑問ですね。さて次の授業でその答えを出していこうと思うのですが、残りの時間は「四角の地図は何が正しい地図なのか」を考えてみて下さい。面積ではありませんでした。面積が違うので距離でもないはずです。何が正しい地図なんでしょうね?そして次回にもつながりますが、それが正しいことを喜ぶ人々によって、世界地図は四角が標準的となったと言えます。誰でしょうか?是非考えてみて下さい。

コメント